| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- Redunancy
- quadruped
- legged robot
- 여자유도 로봇
- Robotics
- 4족 로봇
- inverse dynamics
- PID control
- 모델기반예측제어
- convex MPC
- MPC
- null space
- Model Predictive Control
- ascento
- Disney robot
- Quadratic Programming
- pid 제어
- control
- 널스페이스
- 최적 제어
- 경로 계획
- Optimal control
- time delay compensation
- 시간 지연 보상
- 제어
- 테스크 스페이스
- path planning
- 모델 예측 제어
- task space control
- 여자유도
hyein's 로봇 알고리즘 연구소
한번에 읽는 Robotics Overview 본문
안녕하세요. 블로그를 시작하고 첫 포스팅이네요 :)
첫 포스팅으로 어떤 주제로 글을 쓰면 좋을까? 하는 고민이 많이 있었네요. 첫 글인 만큼 특정 주제를 상세하게 다루기보다 전반적으로 로봇 공학 흐름에 대해 이야기드리는 것이 좋을 듯합니다. 혹시 robotics를 수업시간에 배웠지만 큰 흐름을 잊으신 분들이 계시다면 글을 읽고 다시 기억나셨으면 좋겠네요 ^^
아마 다들 학부 수업시간이나 로봇 관련 문헌을 읽다보면 Trajectory Planning(경로 계획), Kinematics(기구학), Dynamics(동역학), Inverse Kinematics(IK, 역 기구학), Inverse Dynamics(ID, 역동 역학)와 같은 용어들을 많이 보고 들으셨을 겁니다. 로봇은 위에서 언급은 용어들로 정의를 할 수 있고, 원하는 궤적대로 로봇을 움직이게 할 수 있습니다.
2 자유도 로봇을 예를 들어 설명드리겠습니다.

로봇의 정의
위 그림을 보면 로봇의 각 링크마다 Frame들이 붙어있습니다. 기구적 수치와 Frame을 바탕으로 DH parameter를 얻을 수 있는데, 이것으로 로봇을 정의할 수 있습니다. 그리고 로봇 Hand 쪽을 end-efffector라고 부르고 $(x, y)$의 집합을 우리는 Cartesian(task) space라고 부릅니다. joint $(q_1, q_2)$의 집합은 joint space라고 부릅니다.
혹시 Ros나 물리 엔진을 사용하신 분들이라면 urdf 파일을 많이 보셨을 텐데, 여기에 로봇이 정의되어 있습니다. 추후에 포스팅에서 로봇을 정의하는 방법에 대해 다뤄볼게요~
로봇 제어
이제 로봇을 제어하는 과정에 대해 살펴보도록 하겠습니다. 일반적으로 원하는 desired input을 주면 plant의 output이 desired input을 따라가도록 feedback제어를 해줍니다. 그럼 이제 요소 하나하나 짚어가 봅시다~

먼저, 로봇이 움직였으면 하는 궤적(A와 점 B 사이의 시간에 따른 궤적)을 로봇에게 말해줘야겠죠? 그것을 구하는 과정이 바로 Trajectory planning입니다.
1. Trajectory Planning
Trajectory planning에 대해 이야기를 하기 전에 먼저 몇 가지 개념들을 짚고 넘어가겠습니다.
로봇이 움직이기를 원하는 점들의 집합을 우리는 path라고 부릅니다. 즉 여기서는 로봇의 초기 위치(점 A)와 마지막 로봇의 위치(점 B)의 집합이 path가 됩니다. 그리고 링크의 길이, 관절의 배치와 같은 기구적인 제한으로 인해 end-effector의 움직임이 제한됩니다. 또, 로봇 관절마다 가동범위가 제한이 되어 있는데 이와 같이 기구적으로 제한된 조건들을 kinematic constraints라고 부릅니다. 관절의 구동계는 최대 토크, 그리고 원하는 최대 속도, 가속도의 조건이 있습니다. 이와 같은 조건들은 dynamic constraints라고 합니다.
우리가 원하는 Path(점 A, 점 B)에 kinematic constraints과 dynamic constraints을 만족하는 시간에 대한 Position, velocity, acceleration을 찾는 문제가 바로 Trajectory planning입니다.

Trajectory는 position, velocity, acceleration의 time history로 로봇이 움직였으면 하는 $x_d$, $\dot {x_d}$, $\ddot {x_d}$ 혹은 $q_d$, $\dot {q_d}$, $\ddot {q_d}$입니다.
2. Kinematics(기구학)
Trajectory planning으로 desired 궤적을 구했으니 이제 로봇에게 명령을 내려야 합니다. 로봇 끝단의 움직임은 로봇의 관절들의 움직임들의 합으로 나타난 결과물입니다. 즉, 로봇을 움직이게 하기 위해서는 end-effector에서의 정보보다 joint space에서의 정보가 필요합니다. 바로, End-effector의 위치, 방향에 대한 정보와 Joint angle사이의 관계를 나타낸 것이 바로 kinematics(기구학)입니다.

Direct(Forward) Kinematics는 Joint Space에서 Task space로의 Mapping을 의미합니다. 즉, 관절의 움직임$(q_1, q_2)$으로부터 end-effector의 위치, orientaion$(x, y)$을 구하는 과정입니다. Inverse Kinematics는 Task space에서 Joint space로의 Mapping을 의미합니다. 즉, end-effector의 위치, orientaion $(x, y)$으로부터 관절의 움직임 $(q_1, q_2)$를 구하는 것을 의미합니다. 만약 desired trajectory가 cartesian을 통해 정의가 되었다면 inverse dynamics를 통해 joint 단에서의 desired trajectory를 구할 수 있습니다. 하지만 joint의 자유도가 end-effector의 자유도보다 많다면 inverse kinematics는 해가 여러 개 존재하는 Singularity 문제가 존재하겠죠?
kinematics에서 등장하는 또 다른 중요한 개념이 바로 jacobian입니다. jacobian은 task space를 X를 joint space의 q로 편미분 한 결과입니다. 식 (1)을 정리하면 식 (2)와 같은 형태가 되는데, jacobian이 end-effector의 속도와 joint의 속도 사이의 관계를 나타내 줍니다. jacobian이 중요한 이유가 (3)에 있습니다. jacobian이 end-effector에서의 힘과 관절에서의 토크 값 사이의 관계를 나타내 줍니다. 이를 이용하면 end-effector에서의 desired 힘이 있다면 jacobian을 통해 desired 조인트 토크를 계산할 수 있습니다.
$J = {\partial {X} \over \partial {q}}$
$\dot {X} = J\dot {q}$
$\tau = J^T(q) F$
3. Dynamic Model
자, 로봇의 joint space에서의 desired 값을 구했으니 이제 로봇 관절의 구동계가 그 궤적을 따라가도록 제어를 해야 합니다. 로봇 모델 기반으로 제어하기 위해서는 먼저 로봇의 동역학 모델을 알아야 합니다. 로봇의 동역학 모델은 아래와 같이 표현됩니다.
$M(q)\ddot {q} + C(q, \dot {q}) + G(q) = \tau$
$\ddot {q} = M(q)^{-1}(\tau - C(q, \dot {q}) - G(q))$
$M(q)$ : inertia matrix , $C(q, \dot {q})$ : coriolis and centrifugal force matrix, $G(q)$ : gravity matrix, $\tau$ : torque term
로봇의 동역학 모델은 Euler-Newton method 혹은 Euler-Lagrangian method를 사용하여 얻을 수 있습니다.
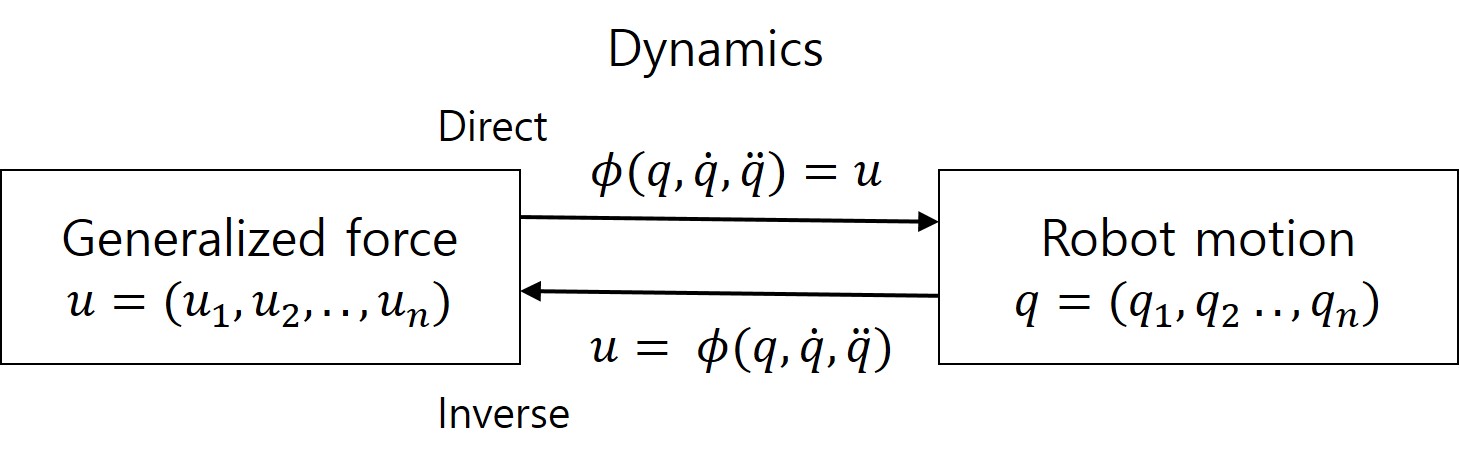
Direct(forward) dynamics는 힘/토크를 가했을 때 로봇의 움직임 결과(joint variable)를 의미하고, Inverse dynamcis는 원하는 motion을 얻기 위해 필요한 힘/토크를 구하는 것을 의미합니다.
4. Control
자 이제 거의 마지막 단계입니다. Plant의 모델도 구했으니, 이를 바탕으로 제어기를 설계해야겠죠? 제어기는 plant모델의 선형, 비선형에 따라 선형 제어기부터 비선형 제어기가 있습니다. computed torque control, Impedance control, Sliding mode control, linear quadratic regulator control, model predictive control 등이 있습니다.
언급한 제어기들은 차후 포스팅을 통해 자세히 알려드리도록 하겠습니다~
5. Trajectory와 forward kinematics 결과 비교
마지막으로 desired input이 cartesian이라면, cartesian에서의 desired trajecotry와 joint space에서 정의된 plant의 output을 forward kinematics를 통한 결과와 비교를 해보아야겠죠?
자, 이제 로봇 공학에서의 큰 흐름들이 다시 정리가 좀 되시나요? 각각 요소별로 깊게 다루지는 못했지만 앞으로 toy project들을 통해 위에서 언급한 내용들을 다루어 보도록 하겠습니다.
'Robotics Algorithm' 카테고리의 다른 글
| Null space를 이용한 Task Space Control 시뮬레이션 (8) | 2022.03.10 |
|---|---|
| Redundant robot에서 Null Space Projection의 개념 (6) | 2022.03.07 |
| Kinematics(기구학) 1편 - Coordinate transformation(좌표 변환) 뽀개기 (6) | 2020.08.26 |



