| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 4족 로봇
- quadruped
- 여자유도 로봇
- Quadratic Programming
- Optimal control
- inverse dynamics
- legged robot
- pid 제어
- task space control
- null space
- control
- MPC
- 최적 제어
- Model Predictive Control
- 테스크 스페이스
- path planning
- PID control
- 모델 예측 제어
- ascento
- 경로 계획
- 여자유도
- Disney robot
- time delay compensation
- 널스페이스
- 제어
- Redunancy
- convex MPC
- 시간 지연 보상
- 모델기반예측제어
- Robotics
hyein's 로봇 알고리즘 연구소
Kinematics(기구학) 1편 - Coordinate transformation(좌표 변환) 뽀개기 본문
Kinematics(기구학) 1편 - Coordinate transformation(좌표 변환) 뽀개기
hyein14 2020. 8. 26. 22:00안녕하세요. hyein's 로봇 알고리즘 연구소의 세 번째 글이자, 첫 연재 시리즈네요!ㅎㅎ 첫 연재는 Coordinate transformation(좌표 변환)에 대해서 다루어 보려고 합니다.
로봇을 설계하거나 혹은 제어를 할 때 빼놓을 수 없는 개념이 바로 Kinematics(기구학)입니다. Kinematics(기구학)에서 '좌표계 도입'과 '좌표간의 변환'은 핵심적인 내용이지요. 물론 로봇 뿐만 아니라 IMU(관성 센서)를 사용하는 분들이나 항공(비행기, 드론 등)을 다루는 분들에게도 굉장히 중요한 개념이기도 합니다.
자, 그럼 좌표계에 대해서 한번 같이 알아볼까요? 혹시 아직 '한번에 읽는 robotics overview'를 보지 않으셨던 분들이 계시다면, 아래 글도 함께 읽어본다면 로보틱스의 큰 흐름을 파악하는데 도움이 될거라고 생각합니다.
2020/07/16 - [Robotics Algorithm] - 한번에 읽는 Robotics Overview
한번에 읽는 Robotics Overview
안녕하세요. 블로그를 시작하고 첫 포스팅이네요 :) 첫 포스팅으로 어떤 주제로 글을 쓰면 좋을까? 하는 고민이 많이 있었네요. 첫 글인 만큼 특정 주제를 상세하게 다루기보다 전반적으로 로봇
hyein-robotics.tistory.com
하기의 그림들은 Craig 저 'Introduction to Robotics' 에서 발췌했습니다.
1. 왜 좌표계를 사용할까?
로봇을 다루는 데 왜 좌표계가 필요할까요? 만약 여러분들이 로봇 팔에게 테이블에 놓인 사과를 집도록 명령을 내린다고 가정해 보겠습니다. 그러면 로봇에게 1) 현재 위치에서 사과까지 떨어진 거리(translation)과 2) end-effector의 방향(orientation)을 알려주어야 사과를 집을 수 있겠죠? 바로 위치와 방향를 표현하기 위해서 좌표계를 도입합니다.
기준 좌표계를 잡고, 관심이 있는 물체에 새로운 좌표계를 부착합니다. 그러면 기준 좌표계에 상대적으로 물체에 부착된 다른 좌표계의 위차와 방향을 표현할 수 있습니다.
2. Rotation Matrix(회전 행렬)
그럼 orientation(방향)에 관련된 내용부터 같이 살펴 보도록 하겠습니다. 아래 그림을 보면, 원점을 공유하는 Frame {A}와 Frame {B} 그리고 점 P가 있습니다. Frame은 기준 좌표계로부터의 위치와 방위를 가진 집합입니다

Frame {A}의 basis는 ${(\hat{X}_A, \hat{Y}_A, \hat{Z}_A)}$, Frame {B}의 basis는 ${(\hat{X}_B, \hat{Y}_B, \hat{Z}_B)}$입니다. 자 그럼 Frame {A}, Frame {B}에 대해 점 P를 표현해 봅시다.
1) Frame {A}의 좌표계를 기준으로 점 P를 표현

2) Frame {B}의 좌표계를 기준으로 점 P를 표현

Frame {A}와 Frame {B}는 원점을 공유하고 있으므로 어떤 좌표계로 바라보던 간에 원점에서 점P를 나태는 것은 동일합니다. 그렇다면 Frame {A}에 대해 나타낸 점 P의 각 성분들을 Frame {B}에 대한 점 P표현식으로 대입할 수 있습니다.

그럼 다음과 같은 식을 얻을 수 있습니다.

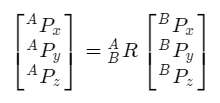
마지막 식을 잘 살펴보면, Frame {B}에서 표현된 점 P가 Rotation Matrix(회전 행렬) ${}^{A}_BR$을 통해 Frame {A}에서 바라보는 점 P로 변환되었죠? 이를 Frame {B}에서 Frame {A}로 ${}^{A}_BR$을 통해 Mapping 되었다고 말합니다.
Rotaion Matrix(회전 행렬)의 각 성분은 단위 벡터들의 내적이므로, 각 성분들은 두 벡터 사이 각도의 코사인 값을 갖습니다. 즉, 각 성분은 단위 코사인(direction cosines)으로 이루어져 있으며 각 성분의 크기는 1과 같거나 1보다 크지 않습니다.
또, Rotation Matrix(회전 행렬)의 각 컬럼들이 orthonormal이기 때문에 아래와 같은 특징을 만족합니다.

자 그럼 위의 내용들을 예제를 통해 한번 알아보도록 하겠습니다.
Ex) Frame {B}가 Frame {A}에 상대적으로 30도 회전해 있습니다. 그렇다면, Frame {B}로 표현된 점 P를 Frame {A}에 대해 점 P를 표현한다면 어떻게 될까요?

Rotation Matrix(회전 행렬)의 요소들을 살펴보면 다음과 같이 됩니다.

이 식을 정리하면 다음과 같은 Rotation Matrix(회전 행렬)를 얻을 수 있습니다.


Frame {B}에 대해 점 P를 표현한 값이 다음과 같다면, 점 P를 Frame {A}에 대해 표현 하면 다음과 같습니다.

z축에 대한 Rotation Matrix(회전 행렬)뿐만 아니라, x, y에 대한 Rotation Matrix(회전 행렬)도 같은 방법으로 다음과 같이 나타낼 수 있습니다.

3. Translation(전위)
자, 다음은 Translation(전위)에 대해 알아보겠습니다. Frame {A}가 있고 {A}의 원점으로 부터 ${}^{A}P_{BORG}$ 만큼 평행이동만 한 Frame {B}가 있습니다. Frame {B}에 대해 점 P를 표현한 ${}^{B}P$를 Frame {A}에 대해 나타내고자 한다면, 아래 그림과 같이 두 벡터 ${}^{A}P_{BORG}$ 와 ${}^{B}P$를 {${A}$}를 더해주면됩니다. {B}에 대해 나타낸 점 P가 ${}^{A}P_{BORG}$에 의해 {A}에 대해 나타낸 점 P로 Mapping 되었다고 말할 수 있습니다.


4. Transformation Matrix
지금까지 기준 좌표계에 대해 Rotation Matrix(회전 행렬)과 Translation(전위)된 좌표계 사이의 관계에 대해 알아보았습니다. 만약 아래 그림과 같이 Frame {A}에 대해 Rotation과 translation이 동시에 일어난 Frame {B}가 있다면 어떻게 될까요? Rotation과 translation을 동시에 표현해야겠죠?

아래와 같이 표현 할 수 있습니다. Roation Matrix와 꼴이 비슷하죠?

${}^{A}_BT$ 를 우리는 Homogeneous transformation Matrix라고 부릅니다. 자세히 살펴보면 아래와 같습니다.

Rotation Matrix(회전 행렬)의 각 column vector는 orthonormal matrix의 특성으로 인해 inverse matrix가 transpose matrix와 같지만, Transformation matrix의 column vector는 orthonormal matrix가 아니므로 inverse matrix와 transpose matrix가 다릅니다.

5. 로봇 end-effector에서의 Transformation Matrix는?
자, 그럼 이제 로봇에서 위 Transformation Matrix가 어떤 의미를 갖는 지 함께 알아보겠습니다. 앞에서 이야기했듯이 로봇에게 어떤 물체를 집도록 명령을 내리기 위해서는 로봇에게 position과 orientation의 정보를 주어야 합니다. 아래 그림를 보면, 로봇 몸통(Base)에 Frame {Base}, end - effector에 Frame {Tool}이 붙어있습니다.

로봇의 end-effector에 좌표계를 부착할 때 보통 $Z(\vec{a}) $ 는 approach vector , $Y(\vec{s}) $ 는 sliding vector, $X(\vec{n}) $ 는 normal vector 를 나타내도록 부착합니다. 이를 바탕으로 transformation matrix의 rotation matrix의 성분은 end-effector에 정의한 normal vector, sliding vector, approach vector들로 나타낼 수 있습니다.

로봇이 어떤 작업을 한다는 말은 end-effector가 특정한 task를 수행하는 것을 의미합니다. 즉, 위의 Transformation matrix인 ${}^{B}_TT$는 로봇이 반드시 따라가야하는 trajectory를 표현한다고 볼 수 있습니다.
물론, Transformation Matrix가 end-effector뿐만 아니라 로봇의 기구학(링크와 조인트들 사이의 관계)를 나타내는 D_H parameter에 대한 의미도 있습니다. 이는 다음 2편에서 자세하 다뤄보도록 하겠습니다.
6. Orientation에 대한 표현
지금까지 좌표계를 도입하는 이유와 한 Frame에서 다른 Frame으로 Mapping하는 내용에 대해 다루어 보았습니다. 마지막으로 Orientation을 표현하는 방법들에 대해 좀 더 살펴보도록 할께요.
Orientation을 나타내는 말이 바로 euler 각(roll, pitch, yaw)입니다. IMU(관성센서)나 항공기를 다루셨던 분들은 많이 접해본 용어일 거예요. Orientation을 표현할 때 x 축 회전인 roll 각, y 축 회전인 pitch 각, z축 회전인 yaw각으로 나타냅니다.
저 뿐만 아니라 다른 분들도 roll, pitch, yaw가 헷갈리시는 분들이 계실 텐데, 기억하기 좋은 방법 하나 알려드리겠습니다. 아래 그림을 보면 항공기에 좌표계가 부착되어 있죠? roll은 구르다, pitch는 음정의 높낮이처럼 피치가 올라간다 내려간다라고 기억을 하시면 외우지 않고 이해하기 쉬우실 겁니다.
보시면 roll 방향으로 비행기가 구르는 모양이죠? 그리고 pitch는 비행기의 높낮이가 변하는 것을 볼 수 있습니다.

자, 그럼 roll, pitch, yaw를 표현 하는 두 가지 방법에 대해 이야기해 보겠습니다. 첫 째는 고정된 좌표계에 대해 표현 하는 방법이 있고, 두번째는 현재 좌표계에 대해 표현을 하는 방법이 있습니다.
1) Fixed Frame
Frame {A}는 reference Frame이고, Frame {B}를 ① $\hat{X}_A$에 대해 $\gamma$, ② $\hat{Y}_A$에 대해 $\beta$, ③ $\hat{Z}_A$에 대해 $\alpha$ 만큼 회전을 시킨다면 ${}^{A}_BR$은 어떻게 표현할 수 있을 까요?

아래와 같이 Fixed Frame인 경우는 Pre-Multiplication으로 곱해집니다.

Rotation Matrix로부터 euler angle(오일러 각)은 아래와 같이 구할 수 있습니다. (단, ${cos\beta}$가 0이 되지 않아야하므로 beta는 -90도에서 90도 사이의 값을 가져야함)

2) Current Frame(Z- Y - X Euler angles)
Frame {A}는 reference Frame이고, 최종 Frame을 {B}라고 하겠습니다.
① $\hat{Z}_A$에 대해 $\alpha$만큼 회전시켜 중간 Frame {B'} $\hat{X}_B'$, $\hat{Y}_B'$, $\hat{Z}_B'$가 되었습니다.
② 그리고 현재 좌표계 $\hat{Y}_B'$에 대해 $\beta$만큼 회전시켜 중간 Frame {B''} $\hat{X}_B''$, $\hat{Y}_B''$, $\hat{Z}_B''$가 되었습니다.
③ 마지막으로 현재 좌표계$\hat{X''}_B$에 대해 $\alpha$ 만큼 회전을 시켜 $\hat{X}_B'''$, $\hat{Y}_B'''$, $\hat{Z}_B'''$인 Frame {B}가 되었습니다.
그렇다면 ${}^{A}_BR$은 어떻게 표현할 수 있을 까요?

아래와 같이 current Frame에 대한 회전은 Post - Multiplication 로 곱해집니다.

자, Fixed Frame(고정된 좌표계)에 대한 회전과 Current Frame(현재 좌표계)에 대한 회전에 대해 각각 Pre-Multiplication과 Post-MultiPplication에 대해 알게 되었나요. 오일러 각은 Z - Y - X에 대한 회전 말고도 Z - Y - Z오일러각 등 24가지의 각도 규약이 있습니다.
지금까지 좌표계 변환 및 오일러 각도에 대해 다루어 보았습니다. 많은 도움이 되었으면 좋겠습니다. 혹시 관련하여 다른 질문이 있다면 댓글을 남겨주세요~
다음에는 오늘 배운 개념을 갖고, 다자유도 로봇팔에서 로봇의 configuration을 나타내는 DH parameter와 transformation matrix의 관계에 대해 이야기 해보도록 하겠습니다.
'Robotics Algorithm' 카테고리의 다른 글
| Null space를 이용한 Task Space Control 시뮬레이션 (8) | 2022.03.10 |
|---|---|
| Redundant robot에서 Null Space Projection의 개념 (6) | 2022.03.07 |
| 한번에 읽는 Robotics Overview (6) | 2020.07.16 |



