| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 여자유도 로봇
- PID control
- Disney robot
- null space
- time delay compensation
- 4족 로봇
- inverse dynamics
- Redunancy
- 모델기반예측제어
- Quadratic Programming
- pid 제어
- legged robot
- 여자유도
- 널스페이스
- quadruped
- Robotics
- 최적 제어
- path planning
- ascento
- task space control
- 테스크 스페이스
- convex MPC
- Model Predictive Control
- 모델 예측 제어
- 제어
- 경로 계획
- control
- MPC
- Optimal control
- 시간 지연 보상
hyein's 로봇 알고리즘 연구소
Matrix Augmentation을 이용한 시간 지연 보상법 (TDC, time delay compensation) 본문
Matrix Augmentation을 이용한 시간 지연 보상법 (TDC, time delay compensation)
hyein14 2021. 11. 3. 23:03안녕하세요. 오랜만에 글을 작성하네요. 최근에 제 블로그에 구독을 눌러주시는 분들도 생기고, 방문자수도 많이 늘어나서 굉장히 기쁘네요. ^^ 힘을 내서 여러분들에게 도움이 될만한 글도 많이 적고, 개인 프로젝트도 계속 진행해 나가면서 얼른 근황도 올려야겠습니다.
오늘은 재미있는 주제에 대해 이야기를 해보고자 합니다. 로봇 제어를 하면 보통 다음과 같 큰 흐름으로 이루어집니다.
먼저 1) 로봇 모델(equation of motion, 운동 방정식)을 구하고
2) 로봇 모델을 기반으로 제어기를 설계합니다.
3) 시뮬레이션에서 desired 값을 만족하는 제어기 설계가 잘 이루어졌다면, 이를 기반으로 실제 로봇에 포팅을 합니다.
이때, 마지막 3단계 포팅에서 만나는 문제에 대해 이야기를 해보고자 합니다.
글의 흐름은 아래와 같습니다.
1. 이론(Simulation)과 현실(Real) 모델의 차이
2. 시간 지연(time delay)가 안정성(stability)에 미치는 영향
3. 시간 지연 보상(TDC, time delay compensation)
4. 한계점
1. 이론(Simulation)과 현실(Real) 모델의 차이
이론(Simulation)과 현실(Real) 모델의 차이는 불확실성(uncertainty)때문에 나타납니다. 불확실성(uncertainty)란 로봇의 치수(dimension), 관성 분포, 마찰, 댐핑, 액츄에이터의 데드타임(dead time), 액츄에이터의 시상수, 통신의 지연 등이 있습니다. 기구적인 모델링 문제나 마찰과 댐핑을 제외 한다면, 대표적으로 현실과 시뮬레이션의 가장 큰 차이는 모터 모델 반영 유무와 컨트롤 law에 의해 계산된 토크 값이 지연 유무 입니다.
만약 이상적인 상황이라면 아래와 같은 식으로 우리는 로봇 모델을 표현 할 수 있습니다. 현재 시간 t 일때, 바로 토크가 모델에 반영이 됩니다.

위와 같은 상황은 그림1의 검은 점선인 Simulation(Ideal)일 때의 그림으로 나타낼 수 있습니다. 하지만 실제 엑츄에이터는 시상수를 갖고 있으므로 바로 step input을 따라가지 못하고 어느 정도 시간이 지난뒤 수렴을 합니다. 즉, 빨간 실선인 Real Actuator /wo dead time으로 표현할 수 있습니다.
그리고 앞에서 이야기를 했듯이 통신의 지연등의 문제로 액츄에이터에 데드타임이 존재하게 된다면, tau 초가 지난 후에 모터가 움직이게 됩니다. 즉, 식은 다음과 같이 표현이 가능합니다.


2. 시간 지연(time delay)가 시스템 안정성(stability)에 미치는 영향
시간 지연(time delay)가 발생하면, system의 안정성에 과연 무슨 영향을 미칠까요? 이를 위해서는 먼저 시간 지연에 대해 알아보도록 하겠습니다. 시간지연을 전달함수(transfer function)으로 표현하면 ${\exp(-s\tau)}$로 표현이 됩니다. 만약 시간지연이 있다면, 시스템 G(s)앞에 시간 지연이 아래와 같이 붙습니다.

시간 지연 부분을 bode plot으로 나타내보겠습니다.

오~ 두 가지 특징이 보입니다. 1) Magnitude 값이 모든 주파수 영역에서 일정합니다. 2) Phase가 주파수가 증가함에 따라 무한히 감소하고 있습니다. 이 두 가지 특징을 고려해보면 시간 지연(time delay)가 반영된 시스템은 Magnitude의 변화는 없이 Phase가 시간 지연이 없는 시스템보다 더 phase가 지연 됨을 알 수 있습니다. 이를 해석해보자면 gain margin이 감소한다고 볼 수 있습니다.
만약 우리가 모델을 기반으로 margin이 확보된 제어기를 설계했다고 하더라도, 실제 포팅 시 기구적인 model uncertainty로 인해서도 확보한 marign이 줄게됩니다. 여기에 time delay가 있다면, margin이 역시 감소하여 전체적은 system은 unstable해질 수도 있습니다.
3. Matrix Augmentation을 이용한 시간지연보상 (TDC, time delay compensation)
시간 지연을 보상하는 방법은 크게 1) 스미스 필터와 2) 지연된 제어 인풋(control input)를 state에 추가하여 Matrix Augmentation을 통해 보상하는 방법이 있습니다. 오늘 여기에서 다루어볼 내용은 후자입니다.
위에서는 연속 시간(Continuous time)에 대해 표현을 했지만, 실제 포팅을 할 때는 이산화(discretization)을 통해 이산 시간(Discrete time)에 대해 표현하기 때문에, 지금부터는 discrete model을 기반으로 이야기를 진행하겠습니다. 지연이 포함된 모델의 discrete model은 다음과 같습니다.
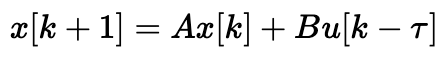
여기서 각 행렬의 차수(dimention)은 A : n x n, B : n x m 입니다.
자, discrete model이 구해졌습니다. 그림 3을 보면 1 ~ tau 만큼 지연된 제어 인풋들을 기존 state인 x[k] 에 추가한 상태인 ${x_{aug}[k]}$를 만듭니다. 이를 바탕으로 ${A_{aug}}$ 와 ${B_{aug}}$를 구해보면 그림 3과 같습니다.

위와 같이 새롭게 augmented된 matrix를 바탕으로 feedback control gain, K을 구하면 됩니다. 가장 쉬운 방법은 margin이 최적으로 확보되 있는 lqr gain K를 사용하는 것이 좋습니다.
4. 한계점(Limitation)
지금까지 matrix augmentation을 통해 time delay를 보상하는 simple한 방법에 대해 알아 보았습니다. 시간 지연의 갯수만큼 state에 augmented를 하기 때문에 계산양이 많아집니다. 특히 sampling time이 높은 경우 일정 시간 지연을 보상하기 위해 더 큰 state의 수가 필요합니다. 그럼에도 불구하고 상대적으로 낮은 샘플링과 적은 matrix size에서는 시간 지연을 보상하기에 좋은 접근 방법입니다.
'Robotics Control Theory > Morden Control' 카테고리의 다른 글
| Sliding mode control (SMC, 슬라이딩 모드 제어)란? (59) | 2021.03.04 |
|---|

